The continuing story of “Saving our Skins”. Here I answer the question: why do we care? There’s a bit of science involved, but hopefully it’s not too heavy.
Updated September 5, 2021.
Why do we even care about ozone? It represents only a tiny fraction of what’s in the air. If you could take all the air above you and compress it into a layer at the pressure of the Earth’s surface, it would occupy a depth of about 8 km whereas, as I mentioned in chapter 9, if you did the same to all the ozone in the air - that layer would be only 3 mm deep. So, for every ozone molecule there are nearly 3 million other molecules of air. In other words, the average mixing ratio of ozone in air is less than 0.4 parts per million (ppm). And the vast majority of it is more than 15 km above us, high in the stratosphere.
It’s a slightly bluish gas with a strong distinctive smell. In fact its name comes from the Greek ozein, to smell. You’ve probably noticed the pungent smell if you’ve ever done a lot of photocopying in a confined space. The ultraviolet light in the photocopier can break oxygen molecules apart to form ozone. And it’s poisonous. That makes it our enemy low down in the atmosphere where we live. Luckily, it’s not normally a health issue because background levels of ozone are usually small near the Earth’s surface - about 20 parts per billion (ppb). But in polluted cities like Los Angeles, photo-chemical reactions in smog can lead to dangerous levels. Health warnings are issued there when its concentration exceeds a danger threshold of 100 ppb. Although the smell of ozone can be detected by some at background levels, a strong smell may indicate that its concentration is dangerously high. Make sure your photocopying room is well ventilated.
But while ozone is harmful in the air we breathe, its much greater concentrations higher in the atmosphere serve a crucial purpose by protecting us from harmful UV radiation from the Sun. Without ozone, life as we know it could not exist.
The dispersed spectrum of white light that’s visible to our eyes shows the familiar splitting into the colours of the rainbow from violet (wavelength 400 nm) through to red (700 nm).

The full spectrum of incoming energy from the Sun extends far beyond that visible range, to include wavelengths down to 100 nm in the ultraviolet (UV) region, and out beyond 5000 nm (5 microns) in the infrared (IR) region.
The total radiation from the Sun reaching the Earth’s surface can exceed 1,000 Watts per square meter (i.e., 1 kW m-2), which is about the same as having one small electric heater for every square metre of ground. But only around 40 percent of that is within the range of visible light. The remaining 60 percent of the energy is at wavelengths we can’t see, with more than 50 percent at longer infra-red wavelengths, and about 5 to 10 percent (up to 100 Wm-2) at shorter UV wavelengths less than 400 nm.
Most of the visible radiation is transmitted to the Earth’s surface, which is why the human eye evolved to use those wavelengths that we call “light”. In that region, absorption lines from gases in the sun’s atmosphere are the only significant absorption features in the spectrum. They’re called “Fraunhofer” lines, named after their German discoverer. The absorptions near 450 nm that we’d used to measure nitrogen dioxide (as discussed in chapter 3), are much less than 1 percent.
But outside the visual range, the atmosphere is less transparent. While about 70 percent of the solar infra-red still gets through, only a small fraction of the UV reaches the ground. The UV part of the spectrum is arbitrarily subdivided in 3 sub-regions: UV-A (315 -400 nm), UV-B (280-315 nm), and UV-C (100-280 nm). UV-A is hardly affected by ozone, and UV-C is completely absorbed by ozone and oxygen molecules in the atmosphere.
It’s the UV-B radiation that’s harmful to life on Earth. Outside the Earth’s atmosphere about 17 Wm-2 of solar radiation falls in the UV-B range. But it’s strongly absorbed by ozone in the light path traversed through the atmosphere, making it highly variable at the surface.
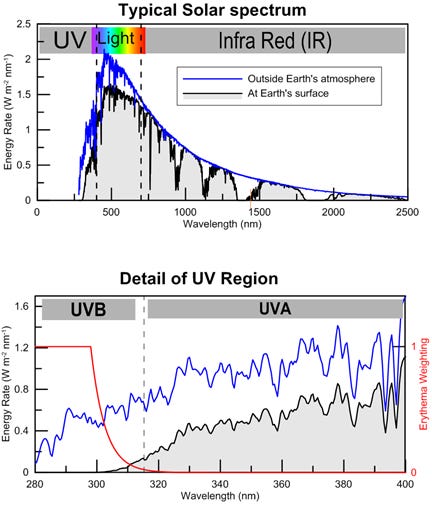
Because of the increasingly strong absorption by ozone at shorter wavelengths, hardly any energy at wavelengths less than 300 nm reaches the surface. Typically, only 1 to 10 percent (usually less than 2 Wm-2) of the total UV-B gets through to the ground at midday, and a much smaller fraction when the Sun is lower in the sky. So UV-B radiation at the Earth’s surface is a tiny fraction of the total energy from the Sun (less than ~0.2 percent).
Despite that, it has the capacity to wreak havoc. You can think of solar energy - including light - coming in a stream of tiny “bullets” of energy. We call them “photons”, where the amount of energy per photon is inversely proportional to its wavelength. So a photon of orange-coloured light with wavelength 600 nm has only half the energy of a photon in the UV region at 300 nm. Although there aren’t nearly as many photons at these UV wavelengths, each has enough energy to break the chemical bonds that hold together molecules of DNA, the building blocks of life. The resulting damage to DNA can be the first step in the development of skin cancer. The peak output from the Sun occurs at visible wavelengths, so the stream of photons is largest there. But the photon energies at those wavelengths are not sufficient to damage DNA. The shorter the wavelength, the greater the energy, so the greater the probability of damage from each impacting photon.
Within the UV-B range, absorption by ozone becomes stronger and stronger at shorter wavelengths. Consequently, the radiation transmitted to the Earth’s surface decreases more than one thousand times over that same short wavelength range, making it extremely difficult to measure accurately, especially at the shortest wavelengths. No broadband instrument can have a passband that exactly matches those limits, so approximations and corrections are needed. Even using results from spectrometer readings measuring at high spectral resolution and integrating over the UV-B wavelength range poses problems because the spectral integral is so heavily dominated by the longest wavelengths. To make matters worse, there’s no universal agreement on the boundary between UV-A and UV-B. Officially, it’s at 315 nm, but some groups prefer to use 320 nm. For that boundary what might still be called UV-B would be about twice that for the 315-nm boundary.
To avoid these problems, we often report the amount of UV in biologically relevant terms. For example, in terms of its ability to damage DNA. For that, you need to know how its sensitivity to damage varies with wavelength. Experiments have been done to calculate this and form what’s called the “weighting function” or “action spectrum” for DNA-damage. As expected, it’s a function that decreases steeply through the UV-B region.
But not many of our own DNA molecules are exposed directly to UV light. They are buried under our skin, and other action spectra that take the transmission of skin into account will be more appropriate for human health. Our main concern about UV is its effect on skin cancer. It would be nice to have an action spectrum for induction of skin cancer, but in practice it’s hard to get that information. There’s the obvious ethical problem of deliberately trying to give subjects skin cancer during the experiment, and there’s also the more practical reason that skin cancers don’t develop immediately after exposure. It usually takes decades. Other animals, like mice that have been genetically modified to increase their susceptibility to UV damage, are sometimes used as a substitute for human subjects. But can we presume that effects seen there would be the same as for unmodified humans? Maybe not.
Instead, the action spectrum for causing sunburn (or erythema, as it’s more properly called) is often used. And we further assume that the same function can be used as a proxy for the risk of developing skin cancer. In 1987, just as the ozone problem was emerging, a Scottish scientist, Brian Diffey, published his weighting function for UV damage to skin that showed the relative importance of different wavelengths in causing sunburn. His weighting function is called the erythemal action spectrum. It ranges from an arbitrary normalisation value of 1 for wavelengths up to 297 nm, then reducing steeply to a value of 0.0001 at 400 nm. In other words, a photon of wavelength 297 nm has 10,000 times the sun-burning effect of one at 400 nm.
Diffey’s erythemal weighting function has become the de facto standard for UV reporting. His paper describing it is probably the most-cited in my research field. It’s often mis-cited, unfortunately, and it’s my fault. In a sign of the times, my copy of his paper at Lauder had been photo-copied and faxed to me by our head-office librarian. When I entered the reference details, I misread the name of one of the editors. The error wasn’t too serious, unless your name happens to be Passchier. The correct reference is:
A.F. McKinlay and B. L. Diffey, A reference action spectrum for ultra-violet induced erythema in human skin, in Human Exposure to Ultraviolet Radiation: Risks and Regulations eds.: W. F. Passchier and B. F. M. Bosnajakovic, Elsevier, Amsterdam, 1987, pp. 83-87.
But I’d mistakenly transcribed the “i” in Passchier’s name as “l”. Later I used the incorrect reference in a widely read Ozone Assessment report. The error migrated via that route into many subsequent papers.
Diffey’s erythemal weighting function was illustrated by the red line in the last graph. It’s also shown by the grey line in the upper graph below. There, a log scale is used for the y-axis as is common in the UV region where the range of irradiances is too large to be seen clearly on a linear scale.

In sunlight reaching the Earth’s surface, the largest contribution to erythemally-weighted UV is from wavelengths near 305-310 nm in summer, but from slightly longer wavelengths in winter. At shorter wavelengths the solar spectrum becomes too small, and at longer wavelengths the weighting function becomes too small, as shown below.
We later showed, in a paper published in 2004, that for a wide range of conditions erythemal UV is a factor of 7.5 smaller than unweighted UV-B (assuming an upper wavelength boundary at 315 nm). So, whereas the maximum UV-B reaching the Earth’s surface at sea level is about 3 Wm-2, the corresponding maximum erythemal UV is only 0.4 Wm-2. It’s a tiny fraction of the total solar energy, but important because photons at those wavelengths can damage DNA.
We were right to be concerned about ozone. If there were none in the atmosphere above us the peak UV-B reaching the surface would be three times as high and sun-burning UV would be twenty times as high as the numbers quoted above. And the intensities of UV at wavelengths less than 300 nm would be thousands of times greater. The effects from these short wavelengths on skin cancer are unquantified. But they are probably massive based on our knowledge of the damage caused by radiation from longer, less energetic wavelengths.
The UV Index (UVI), which was introduced a decade later, is just a scaled version of erythemal UV. A value of 0.25 Wm-2 corresponds to UVI = 10 (extreme), and the maximum at sea level of about 0.4 Wm-2 corresponds to UVI = 16.
Ozone depletion was far from just an academic issue. If depletion in populated areas were ever to become as severe as in the Antarctic spring, maximum UVI values could more than double, no doubt with corresponding increases in skin cancer.
If we couldn’t fix the hole in the Earth’s outer skin, we faced a grim price to be paid through damage to our own skin. We needed to learn more.
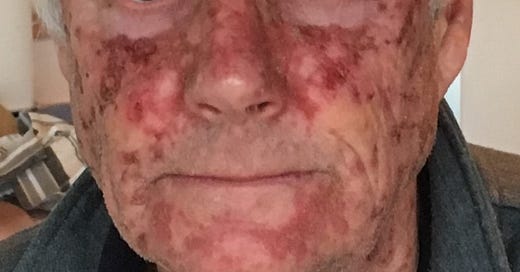
It would be personal for me. In the photograph below, the original skin damage that led to the need for the treatment was from accumulated UV exposure, especially in the 1960s and 70s when I spent a lot of time working outdoors without protection during my school and university summer vacations. At that time the risks of long-term skin damage from UV weren’t known (at least to me). I have to admit that a photo a couple of days after that one showed even worse effects, but I couldn’t bring myself to use that one. Fortunately, my face made a full recovery in a couple of weeks.
[1] The spectrum shown at the Earth’s surface is a reference one (ASTM G-173) used by the American Society for Testing and Materials to represent the mean noon irradiance in the contiguous USA. The Sun elevation angle is 41.8 (airmass = 1.5), with the plane of incidence oriented towards the Sun (rather than the usual horizontal). It assumes cloudless skies, with clean air (optical depth 0.084 at 500 nm), ozone 342 DU, and 14.2 mm of precipitable water, which is relatively dry. Most of the IR absorptions in the upper panel are due to water vapour.
Next week. The beginnings of UV research at Lauder …