The biggest mistake ever?

Reported UVI exceeds reality by more than forty orders of magnitude ...

I’ve been involved with atmospheric measurements for a long time. In that quest, scientists like me are always striving to improve accuracy. The higher the accuracy, the more useful it is, and the greater the cost.

If you ask any atmospheric scientist how much ozone is overhead at any time, most should be able to tell you, with an uncertainty of better than plus or minus 50 percent, that it’s about 300 Dobson Units (where 1 Dobson Unit is equivalent to an overhead column of ozone amounting to 2.69x10^16 molecules per square centimetre of area). We know that, because that’s the global average, and outside the springtime Antarctic ozone hole (more about that in the next week or two) the natural range of ozone is from about 200 to 450 Dobson units.

There’d be no cost for that estimate. If you want its accuracy to 10 percent instead of 50 percent, you need to use a measurement, probably from a satellite-borne instrument, unless you happen to be an an atmospheric research station where ground-base measurements are available. But, even the best instruments in the world, costing tens of thousands of dollars, can’t do it to better than 1 percent accuracy, meaning that an ozone measurement reported as 300 DU really means it’s somewhere between about 297 and 303 DU.

It's even harder to estimate the UV Index (UVI). In addition to its well-known dependence on ozone, it also depends many other factors, starting with the amount of UV radiation emitted by the Sun. That depends on solar activity which has an 11-year cycle, and varies spatially on the solar surface, so we see a 27-day cycle in radiation in concert with the Sun’s rotation on its axis. Then there’s the seasonal variability in Earth-Sun distance. Those factors alone lead to variations in UVI exceeding 7 percent before it even reaches our atmosphere.

Extinctions by ozone and other atmospheric constituent cause much larger reductions in UVI. Even the air itself causes losses because of the efficiency of tiny air molecules at scattering radiation - and especially UV radiation - out of the direct beam of sunlight. Consequently, these losses depends on the path-length of light through the atmosphere, and therefore on the Sun’s elevation angle (which depends on latitude, season and time of day). The amount of air to be traversed also depends on atmospheric pressure, which is affected by weather patterns, but is governed mainly by the height of the surface above sea level. Even the reflectivity of that surface in the UV region has to be considered because some light that’s reflected by the surface gets scattered back down again by those air molecules. Not many surfaces reflect UV radiation efficiently, but reflections from snow-covered surfaces can be responsible for UV increases exceeding 20 percent – and are therefore a significant factor leading to sunburn for snow-skiers.

So its complicated. And that’s all just for clear-sky UV. Most of the time, clouds hugely modify the clear-sky UVI. Usually they reduce it, sometimes cutting it back by 90 percent or more; but reflections from the edges of scattered clouds can also increase it by up to 20 percent or so for shorter periods. Then there’s the effects of air pollution. Even in even in supposedly clean air, extinctions from aerosols suspended in the atmosphere can reduce the UVI by 20 percent or more. And in polluted cities the reductions can be much larger.

Our bodies have no sensors to tell us how much UV there is. Our eyes might tell us that the radiation in mid-winter looks pretty similar to that in winter. While that may be closer to the truth in the visible region where eyes are sensitive, it’s far from the truth at UV wavelengths. Where I live, at latitude 45S, the peak UVI in winter is less than 10 percent of that in summer.

Even with decades of experience, I can’t tell you what the UVI is at any place or time to within a factor of two or more. If I restrict it to clear-sky UVI, I’d still be hard-pressed to give the correct answer within 30 percent of the true value, unless I know that the air is unpolluted. In that case, I might be able to achieve an accuracy of 10 to 20 percent, but most would have to use smartphone apps like GlobalUV or UVNZ. If you need better than that, you’ll have to get somebody to measure it. But instruments to do that accurately cost thousands of dollars. The best UV-measuring instruments in the world, costing tens of thousands of dollars, can’t measure UVI to better than 3 percent accuracy.

And just because you spend tens of thousands of dollars, it doesn’t always follow that you’ll achieve anything like that aim in accuracy. I mentioned a couple of examples in my recent posts. I want to talk more about one that produced the largest error I’ve ever seen.

But before that, a confession …

As I mentioned in my book, Saving our Skins, I’ve personally been involved with propagating a pretty large error myself. It wasn’t quite in the same category, but in our first-ever paper on stratospheric trace gases that I published with my colleague Paul Johnston way back in 1982, we included a graph showing the amount of nitrogen dioxide in the atmosphere above Lauder New Zealand (measured in units of molecules per square centimetre). Typical values were 5 x 10^15 molecules per square centimetre. The required label for the y-axis label was rather long, so to save space I naughtily abbreviated ‘molecules’ to ‘mol.’, which is sometimes used as an abbreviation for the word ‘mole’. In the world we live in a mole is a small burrowing animal, or perhaps in the movies an undercover agent. But in the world of atmospheric science, a mole is the number of molecules of gas that occupies a volume of 22.4 litres at standard temperature and pressure. And that’s a BIG number: about 6 x 10^23 molecules (or, if you prefer 600,000,000,000,000,000,000,000 molecules). By using ‘mol’ as an abbreviation for ‘molecule’, we introduced an error - at least to the pedantic - of that huge factor.

…

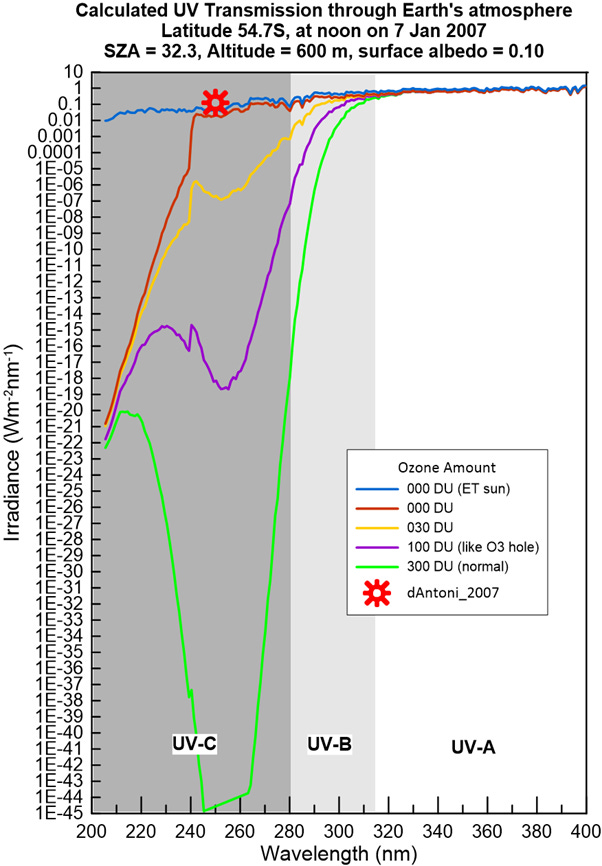
But the error in UV introduced by d’Antoni et al in 2007 left our spurious ‘error’ in its dust, as shown in the plot below, which is just an extension of the one I showed here a few weeks ago. In this version, instead of truncating the y-axis I’ve extended it far enough down so you can see the lower limits in the calculated data.

As you can see, I had to extend it a LONG way down to encompass the values that apply for a mean ozone amount of 300 DU (shown by the green curve). That minimum value near 245 nm is about 44 orders of magnitude smaller than one of their measurements, as shown by the red symbol.  Admittedly, when you get down to numbers that small, you do need to start worrying about whether the numerical precision of the calculation is up to the mark, but even for 100 DU of ozone, which is close to the lowest ever recorded (and there at much higher latitudes where peak solar elevations are much lower), their red point would be too high by 19 orders of magnitude.

From the convergence of the lines at the lowest wavelength, its clear that ozone (O3) is not the cause of the strong absorption there. At wavelengths below 240 nm, the absorption is primarily from the more common form of oxygen (O2). You can see the transition between these by the behaviour of the curves at the lowest ozone amounts (the yellow and purple curves).

Oddly, the authors in that paper from 2007 failed to report the actual ozone at the site that day. But, based on climatological values, it was probably close to the global mean value of 300 DU. In that case, presuming the precision of our calculation was sufficient, the measurement was too high by at least 42 orders of magnitude (i.e., by a factor of 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000). The percentage error is 100 times larger than that  😊.

You’d think they might have become suspicious to see their ‘measured’ value was more that the direct radiation from the Sun measured at that outside Earth’s protective surface (the blue curve). But apparently not …

I don’t know of any bigger error ever. Do you?