UV at low sun elevations: why so small?

Extinctions by ozone and air molecules

After my Facing the Sun post, a reader, Michael Molyneaux, wrote.

it’s still not clear to me why radiation at UVB wavelengths is absorbed to a greater extent by ozone when the sun is low in the sky compared with UVA wavelengths. Is another factor, perhaps light scatter, involved?

Thanks Michael. A very interesting question. It takes a bit of explaining. hope my answer isn’t too arcane.

First, there’s the absorption by ozone. Although most of the ozone is high in the stratosphere - at altitudes between 15 and 40 km - up to 10 percent of it is in the lower atmosphere (i.e., the troposphere). When the sun’s close to the horizon, the pathlength through the lower atmosphere can exceed the vertical pathlength by more than a factor of ten, greatly reducing the amount of UVB, but having little effect on UVA wavelengths where ozone absorption is small. But that’s only part of the story …

There’s another factor involved too. That’s the scattering of light out of the direct beam by molecules of air. It’s called ‘Rayleigh scattering’, which has a very strong wavelength dependence, and results in the light being deflected to different angles of propagation. The scattering efficiency depends on the ratio between wavelength and the diameter of the much smaller air molecules. If you’ll pardon the maths, at visible and UV wavelengths the scattering efficiency is inversely proportional to wavelength (λ) to the power of 4 (i.e., λ^-4).

Whether or not you’re comfortable with the maths, it therefore follows that the amount of scatter at 300 nm (in the UVB region) is greater than at 600 nm (red light) by a factor of 16. Similarly, as I’ve mentioned before, the sky is blue because blue light is scattered about 4 times more than red light. And the sun on the horizon appears reddish because more of the blue has been scattered out of the beam.

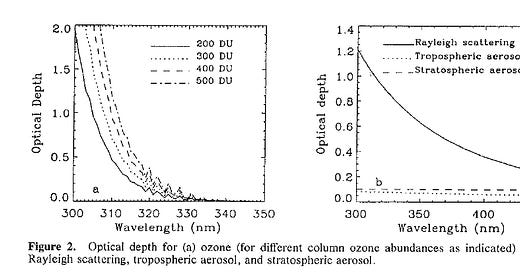
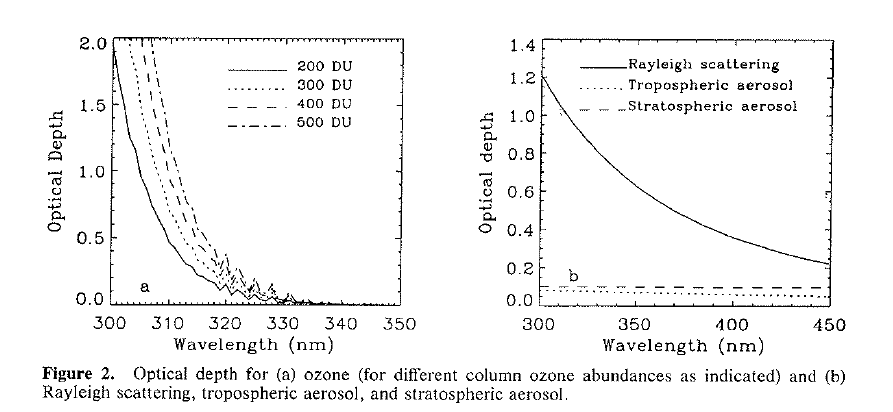
Even within the UV region there are big differences in the amount of scattering by air molecules. Radiation at 300 nm is scattered 3 times as much as radiation at 400 nm. The relative sizes of the ozone effect and the scattering effect are compared in the plots below, which I’ve copied from this paper that we wrote in 1994. They show the ‘optical depth’, which is a measure of how much direct beam radiation is blocked in a vertical path through the atmosphere.

The optical depth, as plotted, has a logarithmic dependence on transmission (that we’re more familiar with). For example, an optical depth of 1 means that about 37 percent (1/e) is transmitted (and the other 63 percent has been scattered). Other examples are shown in the table below.

The left panel of the figure shows that even for an ozone amount as low as 200 DU, the optical depth at 300 nm is 2, which means that 86 percent of that radiation is absorbed. For more typical ozone amounts (around 300 DU), the optical depth at 300 nm would exceed 3, meaning at least 95 percent would be absorbed by the ozone.

The right panel shows that the optical depth due to Rayleigh scattering by air molecules is around 1.2, meaning that about 70 percent of that radiation is scattered out of the direct beam. The dashed curves below show that the optical depths of aerosols are typically much smaller.

Neglecting those aerosols, the total optical depth is the sum of the ozone and Rayleigh optical depths. For 200 DU of ozone, that sum is more than 3, meaning less than 5 percent of the direct beam remains, even for this vertical path. For more typical ozone amounts, the fraction transmitted reduces to less than 2 percent for overhead sun.

If the sun is close to the horizon, the direct-beam’s path length through the atmospheric would be longer by at least a factor of ten. In that case, at 300 nm, virtually all the radiation is scattered. Even 450 nm, where there’s no ozone absorption and Rayleigh scatter is much smaller (optical depth of 2), about 86 percent of the radiation is scattered out of the direct beam.

The net effect is that - although you can clearly see the sun when it’s on the horizon - if your eyes were sensitive only to UVB wavelengths you couldn't see even a vestige of it. Over that long atmospheric path, there’d be several scattering events, so all the radiation you’d see would be from that multiply-scattered skylight coming in from all directions. As in a fog.

Thanks for your question, Michael. I hope my response wasn’t to heavy-going.

Next time it will definitely be lighter …

PS. After my last post, a couple of readers said they’d like to see how my skin lesion looked, a few weeks after the Efudix treatment. I’ve added another image there to show that.