Albedo's just another word for reflectivity

and there ain't much of it in the UVB .....

Sung to the tune of 'Me and Bobby McGee' ….(with apologies to Kris Kristofferson).

UV is different from ‘ordinary’ light as seen by our eyes. As we ‘saw’ recently, most of it comes from scattered skylight, rather than from the direct solar beam. It’s reflection from surfaces is also much lower than for light. Scientists like using complicated words. To them (us!), the reflectivity of a surface is called its ‘albedo’.

Years ago, we had a go at measuring how much UV radiation gets reflected from the ground at different UV wavelengths (i.e., we measured the spectral UV albedo). It wasn’t easy because at the time (last century), instruments to do that properly were quite bulky.

Here’s how our experimental set-up looked for the downward-viewing instrument. It was mounted on a ladder that was cantilevered off the roof of the laboratory. A similar standard upward-viewing instrument was located nearby on the same roof.

A youthful Mike Kotkamp (my colleague who always did all the real work) setting up our spectrometer in February 1995 to measure the up-welling UV radiation. Another nearby instrument simultaneously measured the usual down-welling UV.

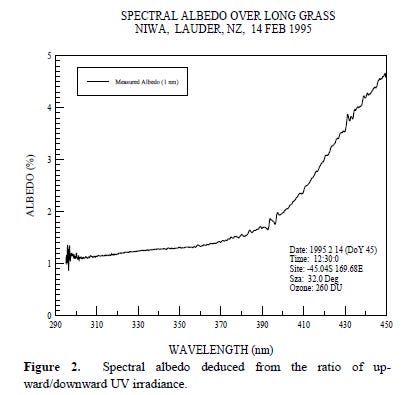
The albedo (i.e., reflectivity, or reflectance) is just the ratio of the downward-looking to the upward-looking measurement. The main result is shown below. The UV reflectance is much less than in the visible region. To our eyes (and the camera in the picture above), the grassy surface looks quite bright. But, as the plot shows, it’s not bright in the UV region. In this example you can see that grass reflects only 1 percent of the incoming UVB (and up to 2 percent in the UVA region).

Results are noisy at the shortest wavelengths. The little glitches at longer wavelengths are due to slight differences in the wavelengths sampled by the two instruments. Notice how the reflection increases rapidly at longer wavelengths. But at the longest wavelength sampled (450 nm), corresponding to violet light, it’s still only 5 percent.

From everyday life experience, we know that the reflectivity is much greater at longer wavelengths where our eyes are most sensitive, such as around wavelength 550 nm, which corresponds to green light. Unfortunately, the instrument we used couldn’t measure that far into the visible.

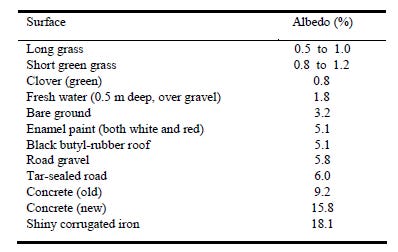
As the table below shows (from the same paper), that grass surface is quite typical for natural surfaces. Very few reflect much UV. The only real exceptions are clouds and snow. Even white paint reflects only 5 percent of the incoming UV - so would look nearly black if our eyes were sensitive to UV wavelengths. But the surfaces of some man-made materials do reflect a bit more UV.

With most UV coming from scattered skylight, and with its lower reflection from natural surfaces, our view of the world would be much different if our eyes were sensitive to that region instead of the visible. It would be like forever living in a fog, with visibility no more than about 10 kilometres (no mountain vistas). A veiled solar disk would be discernible through the fog, but only for high sun elevations. And just about all natural surfaces would look black.

Boring! Thank goodness our eyes are adapted to longer (visible) wavelengths. Much more interesting!